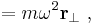Reactive centrifugal force

Classical mechanics
History of classical mechanics · Timeline of classical mechanics
Fundamental concepts
Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle
For the pseudoforce that appears in a noninertial, rotating frame of reference, see Centrifugal force (rotating reference frame).
Illustration of forces between objects – 1: Ball in uniform circular motion held by string tied to post; 2: Centripetal force on ball; 3: Reactive centrifugal force on string and post; 4: Centripetal force on string and ball; 5: Combination of forces on string; the string is in tension; 6: Combination of forces on post – the centripetal force indicated by the red arrow is applied by the post-hole that holds the post.

A reactive centrifugal force is the reaction force to a centripetal force.

A mass undergoing circular motion constantly accelerates toward the axis of rotation. This centripetal acceleration is caused by a centripetal force, which is exerted on the mass by some other object. In accordance with Newton's Third Law of Motion, the mass exerts an equal and opposite force on the object. This is the "real" or "reactive" centrifugal force: it is directed away from the center of rotation, and is exerted by the rotating mass on the object that originates the centripetal acceleration.[1][2][3]

The illustration at right shows a ball in uniform circular motion held to its path by a massless string tied to a post stuck in the ground. Because the string is assumed to be massless, no centripetal force is needed to maintain the circular motion of the string itself. Newton's second law requires that any body not moving in a straight line is subject to a force, and indeed, panel 2 shows the ball is subjected to a centripetal force by the string. Newton's third law states that if the string exerts a centripetal force on the ball, the ball will exert an equal reaction upon the string and post, the reactive centrifugal force shown in panel 3. Panel 4 shows the string and ball combined, both in uniform circular motion. The centripetal force of panel 2 is applied by the post to the end of the string. The string is looked at separately in panel 5, and is subject to a reactive centrifugal force at one end balanced by a centripetal force at the other end, placing the string under tension. Panel 6 shows the post separately. Due to Newton's third law, the post is subject to the reactive centrifugal force, a reaction to the centripetal force of panel 4, and also is subject to the centripetal force exerted by the post-hole on the post. The net force on the post is zero, so it does not move.

Contents

Example: The turning car

See also: Centripetal force#Example: The banked turn
Car with passenger making a turn. The road exerts a centripetal force on the car to force a curved path.
Exploded view showing force components. Each object is subject to a net inward force that is the difference between an inward centripetal force and possibly an outward reactive centrifugal force. This net inward force is the centripetal force upon that object necessary for it to make the turn.

A car with a passenger inside, driving around a curve, provides a good illustration of centrifugal and centripetal forces.[4] The road exerts a centripetal force upon the car, consistent with the car making the turn. This force is called a centripetal ("center seeking") force because its vector changes direction to continue to point toward the center (precisely, the center of curvature) of the car's arc as the car traverses it.

Viewed from an inertial frame of reference, the passenger keeps moving with constant speed and direction as the car begins to turn; that is, failing interference by the car, the passenger is going to travel a straight line, not go around the turn. From this point of view, the passenger is not pushed toward the outside of the path the car follows; instead, the passenger proceeds on a straight path and the car's path curves to meet the passenger. If the seat is slippery, the passenger slides along a straight path across the car seat until meeting the car door, whereupon the door pushes the passenger to follow the curve.

If the car seat is not slippery, it applies a sideways force on the passenger to accelerate around the turn with the car.

If the car is acting upon the passenger, then the passenger must be acting upon the car with an equal and opposite force (Newton's third law of reaction). Being opposite, this reaction force is directed away from the center, as illustrated in the lower figure, therefore centrifugal: this centrifugal force acts upon the car seat, not upon the passenger.[5]

The figure also shows that the car seat is subjected to a centripetal force applied by the car itself. This centripetal force exceeds the reactive centrifugal force exerted on the seat by the passenger, causing the seat to move around the turn under a net inward force. It also shows the car body is subject to the centripetal force from the road, and to the reactive centrifugal force exerted by the car seat. The inward force on the car body exceeds the outward reactive centrifugal force due to the cart seat by enough to make the car body follow the turn.

The sketch shows the forces are not colinear, so they exert a torque on the various parts. Although torque is a likely real-world consideration (the car tends to tip over as it rounds the turn), it simply is ignored here to focus upon the reactive centrifugal force.

The centrifugal reaction force with which the passenger pushes back against the car seat is given by:

\mathbf{F}_\mathrm{centrifugal} \  = - m \mathbf{a}_{\mathrm{centripetal}} \
= m \omega^2 \mathbf{r}_\perp \ ,

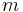where m is the mass of the passenger, 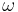\omega the rotational speed (in radians per unit time), and r\perp the radius vector outward from the axis of rotation to the passenger.

The reactive centrifugal force[5] is a real force, but this interpretation of centrifugal force is rarely used in modern discussions.

Applications

Simplified sketch of centrifugal governor consisting of a ball swinging around a post. On the right are shown the forces on the ball due to gravity and the rod. These two forces add by vector addition to form the horizontal centripetal force keeping the ball in circular motion around the post. The rod is in tension in reaction to the ball, and the horizontal component of this reaction force is the reactive centrifugal force. The tension at the top of the rod is supplied by the post.
Simplified sketch of centrifugal clutch. The spring provides centripetal force to the shoe, and the shoe exerts a reactive centrifugal force upon the spring.

Reactive centrifugal force is a real force that can be used to do physical work; a few examples are:

Fictitious forces

Main article: Fictitious force
See also: Centrifugal force and Coriolis force
Reactive centrifugal force Fictitious centrifugal force
Reference
frame		 Any Only rotating frames
Exerted
  by		 Bodies moving in
curved paths		 Acts as if emanating
from the rotation axis,
but no real source
Exerted
  upon		 The object(s) causing
the curved motion,
not upon the body in
curved motion		 All bodies, moving
or not; if moving,
Coriolis force
also is present
Direction Opposite to the
centripetal force
causing curved path		 Away from rotation axis,
regardless of path of body
Analysis Kinematic:
related to
centripetal force		 Kinetic:
included as force in
Newton's laws of motion

When a rotating reference frame is used as reference, an inertial (also known as fictitious or pseudo) centrifugal force appears, in order to make Newton's laws of motion valid in such a frame. That is, the true force on a mass must be supplemented by a (fictitious) centrifugal force that is directed away from the axis of rotation, and also a Coriolis force that bends a moving object's path.

Returning to the example of the car turning, if we consider the reference frame that is rotating together with the car (a model which those inside the car often will find natural), it feels as if a 'magical' force is pushing the passenger away from the center of the bend. In the rotating frame of the car, this push is ascribed to a fictitious force (as opposed to an actual force exerted by another object), an inertial force called centrifugal force. The centrifugal force is invoked by the passengers because the car's acceleration is hidden from observers in the reference frame moving with the car. Nevertheless, in the rotating frame, this type of force appears as real and a natural basis for analysis.[6][7]. See the articles on centrifugal force and fictitious force for examples. Fictitious forces do not appear, however, in inertial frames of reference, in particular, when rotating frames of reference are mapped to inertial frames for the physics.[8].

References

  1. ↑ Delo E. Mook & Thomas Vargish (1987). Inside relativity. Princeton NJ: Princeton University Press. p. p. 47. ISBN 0691025207. http://books.google.com/books?id=QnJqIyk_dzIC&pg=PA47&dq=%22reactive+centrifugal+force%22&lr=&as_brr=0&sig=EDmHHDZRZB4AC37tklWe03SD_tY. 
  2. ↑ Acceleration and force in circular motion by Peter Signell §5b, p. 7
  3. ↑ A. K. Mohanty (2004). Fluid Mechanics. PHI Learning Pvt. Ltd. p. p. 121. ISBN 8120308948. http://books.google.com/books?id=eF-H6O11fdkC&pg=PA121&dq=%22reactive+centrifugal+force%22&lr=&as_brr=0#PPA121,M1. 
  4. ↑ Roger Leslie Timings (2005). Newnes Mechanical Engineer's Pocket Book. Oxford: Elsevier/Newnes. p. p. 111. ISBN 0750665084. http://books.google.com/books?id=IZdDk1cMlLcC&pg=PA111&dq=reactive+%22centrifugal+force%22&lr=&as_brr=0&sig=fg72IYE6vZxgRDWEdTikY5780LE. 
  5. ↑ 5.0 5.1 The Columbia Electronic Encyclopedia: Centripetal force and centrifugal force
  6. ↑ For more detail see Hall: Artificial gravity and the architecture of orbital habitats.
  7. ↑ Hall: Inhabiting artificial gravity
  8. ↑ M. Alonso & E.J. Finn (1992). Fundamental university physics. , Addison-Wesley. ISBN 0201565188. http://books.google.com/books?id=c5UAAAAACAAJ&dq=isbn:0201565188&lr=&as_brr=0. 

External links

See also